Table of Contents
Trees in Data Structure
- It is a non-linear data structure.
- This structure is used to represent data containing a hierarchical relationship between elements.
- E.g. Records, family trees and table of contents.
Tree Terminology
- Root: The root does not have a parent, but each of the other nodes has a parent node associated to it.
- Leaf node: A node that has no children is called a leaf node. Leaf nodes are also called terminal nodes or external nodes.
- Edge or branch: An edge is a connection between vertices. A line from a parent to a child node is called a branch or an edge. If a tree has n nodes, one of which is the root then there would be n – 1 branches.
- Vertex or node: It is a simple object that can have a name and can carry other associated information.
- Siblings: Nodes with same parents are called siblings.
- Internal / Nonterminal nodes: Nodes with alteast one child.
- Path: A path in a tree is a list of distinct vertices in which successive vertices are connected by edges in the tree. There is exactly one path between the root and each of other nodes in the tree.
- Length: The length of a path is the number of branches on the path.
- Depth: The depth of any node n, is the length of the path from root to n. Thus, the root is at depth 0(zero). Depth is also called root.
- Height: The height of a node ni is the longest path from ni to a leaf. All leaves are at height
zero. - Forest: A set of trees is called a forest.
- Degree: No. of children.
General Tree
In a General Tree, parent node can have any no. of child nodes.
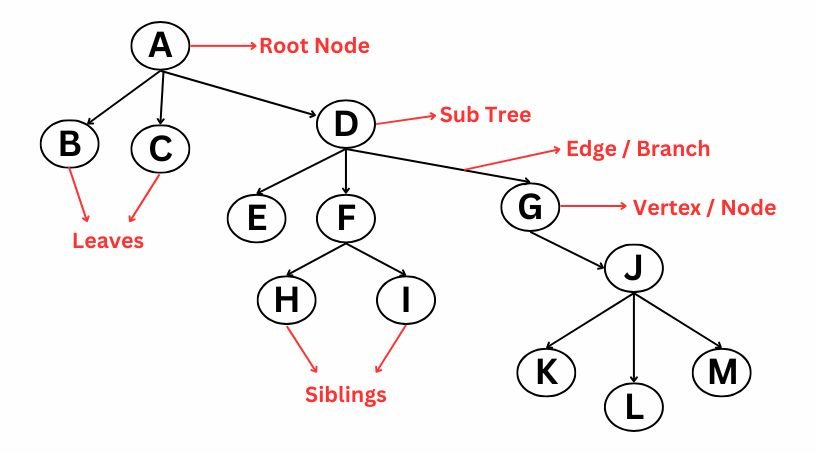
Here,
- Depth(T) = 4
- Degree (Max. no. of children) = 3
- Path from A to K is A – D – G – J – K
- A is ancestor of K and K is descendant of A.
- Height of F is 1 and depth is 2
- Ancestor of F are D and A.
Binary Tree
A binary tree T is a finite (possibly empty) collection of elements when the binary tree is not empty, it has a root element and the remaining elements (if any) are partitioned into two binary trees, which are called the left and right subtrees of T.

Example:
Difference between binary tree and a general tree
Binary Tree | General Tree |
| Binary Tree can be empty. | A General tree cannot be empty. |
| Each element in a binary tree has exactly two subtrees. | General tree can have any no. of subtrees. |
| Subtrees of each element in a binary tree are ordered. | Subtrees in tree are unordered. |
Types of Binary Trees
Full Binary tree: A binary tree of height h that contains exactly 2h – 1 elements is called a full binary tree. All leaves are at same level.
Full Binary tree of height 3.
No. of elements = 2h – 1 = 23 – 1 = 8 – 1 = 7
Within levels, the elements are numbered left to right.
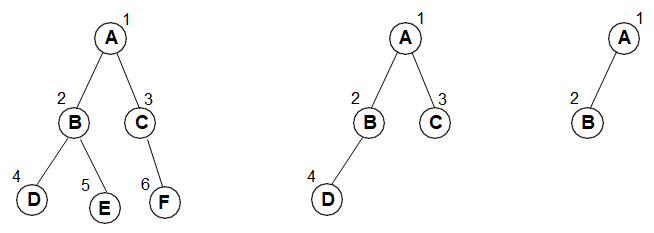
Complete Binary tree: The tree T is said to be complete if all of its levels, except possibly the last, have the maximum number of possible nodes.
Examples:
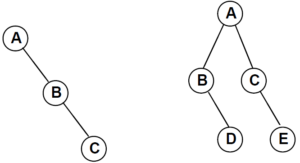
Incomplete Binary trees: Trees which are not complete.
Examples:
Memory Representation of Binary Trees
There are two ways of representing Binary trees in memory:
- Array Representation
- Linked Representation
1. Array representation
The sequential representation scheme to maintain Binary tree “T” in memory, uses only a single linear array which is as follows:
- Root node of tree is stored at position 1 in array.
- If a node n occupies K position in array, then its left child is stored in 2 * K position.
- Similarly, its right child is stored in (2 * K) + 1
Example:
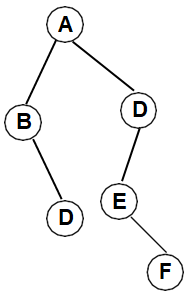
Here, A is root node. So, position = 1 in array
B is left child of A. So, its position = 2 * 1 = 2
C is right child of A. So, its position = (2 * 1) + 1 = 3
D is right child of B. So, its position = (2 * 2) + 1 = 5 and so on.
So, the array representation of above mentioned Binary tree is as follows:

Disadvantages of array Representation:
- The sequential or array representation can be used for all binary trees but in most cases there will be lots of unutilized space. Only for complete binary tree array representation is ideal.
- Operations like insertion or deletion of nodes from the middle of tree require the movement of nodes, which will result into change in level number of these nodes. These problems can be easily solved using linked representation.
2. Linked Representation
In this type of representation each node of a binary tree has three fields:
- info(N), contains the data at the node N.
- Lchild(N), contains the location of the left child of node N.
- Rchild(N), contains the location of the right child of node N.

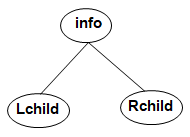
Each element is represented by a node that has exactly two link fields. These link fields known as leftchild and rightchild.
Each edge in the binary tree is represented by a pointer from the parent node to the child node. This pointer is placed in the appropriate link field of the parent node.
There is no link from child node to parent node.
Example:
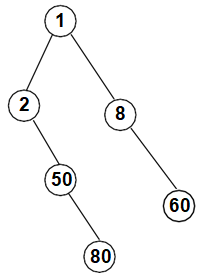
Linked Representation is as follows:

Binary Tree as an Abstract Data Type
ADT Binary Tree
Instances: Collection of elements; if not empty, the collection is partitioned into a root, left subtree and right subtree; each subtree is also a binary tree.
Operations
Create( ): Create an empty binary tree.
Isempty( ): Returns true if empty.
Root(x): x is set to root element.
Maketree(root, left, right): Create a binary tree with root as root element, left as left subtree.
Breaktree(root, left, right): Inverse of Create.
Preorder( ): Preorder traversal of binary tree.
Inorder( ): Inorder traversal of binary tree.
Postorder( ): Postorder traversal of binary tree.
Levelorder( ): Levelorder traversal of binary tree.
Delete( ): Delete a binary tree, freeing up its nodes.
Height( ): Returns the tree height.
Size( ): Returns the no. of nodes in the tree.
Common Binary tree operations
- Determine its height.
- Determine the of elements in it.
- Make a copy.
- Display the binary tree on screen or on paper.
- Determine whether two binary trees are identical.
- Delete the tree.
- If it is an expression tree, evaluate the expression.
- If it is an expression tree, obtain the parenthesized form of expression.
You May Like to Browers More




