Linked List in Data Structure

Definition:

A linked list is a linear collection of data elements, called nodes, where the linear order is given by means of pointers. That is, each node is divided into two parts: the first part contains the information of the element, and the second part, called the link field, contains the address of the next node in the list.

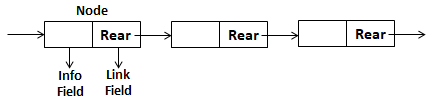
Advantages of linked list:

• Dynamic data structure: The primary advantage of linked list over arrays is that linked list can grow and shrink in size during their lifetime.
• Efficient memory utilization: Here, memory is not pre-allocated. Memory is allocated whenever it is required and it is deallocated (removed) when it is no longer needed.
• Insertion and deletion are easier and efficient: In the link list a data item can be inserted and deleted at a specific position easily.
• Many complex applications can be easily carried out with linked

Disadvantages of linked list:

• Access to a particular data item is little bit complex and time
• Extra memory space is needed for pointer

Operations on linked list:

• Creation
• Traversing
• Insertion
• Deletion
• Concatenation
• Display

Traversing a linked list:

Algorithm: TRAV (INFO, LINK, START, PTR)

This algorithm traverses and displays the elements of linked list. INFO contains the data of the element and LINK contains the address of the next field. Here, PTR is temporary pointer variable used for traversing.

Step 1: [ Initialize the PTR variable. ]

PTR := START

Step 2: [Check whether list is empty or not. ]

If START = NULL then

Write (‘List is empty’)

and return.

[ End of If structure ]

Step 3: Repeat steps 4 and 5 while PTR ≠ NULL

Step 4: [ Display the data. ]

Write ( PTR  →  INFO)

Step 5: [ Move pointer PTR to next node. ]

PTR := PTR →  LINK

Step 6: [ Exit ]

Return.

Counting no. of nodes of a linked list:

Algorithm: COUNTNODE (INFO, LINK, START, PTR, COUNT)

This algorithm traverses and counts the no. of elements of linked list. INFO contains the data of the element and LINK contains the address of the next field. Here, PTR is temporary pointer variable used for traversing. COUNT variable is used to store total no. of nodes

Step 1: [ Initialize the PTR and COUNT variable. ]

PTR := START

COUNT := 0

Step 2: [Check whether list is empty or not. ]

If START = NULL then

Write (‘List is empty’)

and return.

[ End of If structure ]

Step 3: Repeat steps 4 and 5 while PTR ≠ NULL

Step 4: [ Increment the COUNT variable. ]

COUNT := COUNT + 1

Step 5: [ Move pointer PTR to next node. ]

PTR := PTR  →  LINK

Step 6: [ Exit ]

Return.

Insertion of node in linked list:

A. Insertion of node at the beginning

Algorithm: INSBEG (INFO, LINK, START, ITEM, TEMP)

This algorithm inserts TEMP as first node in the linked list. ITEM variable contains data of new node.

Step 1: Allocate memory for new node TEMP.

Step 2: [ Store the ITEM into INFO part of new node ]

TEMP →  INFO := ITEM

Step 3: [ Insert the new node TEMP as first node. ]

TEMP  →  LINK := START

START := TEMP

Step 4: [ Exit ]

Return.

B. Insertion of node at the end

Algorithm: INSLAST (INFO, LINK, START, ITEM, TEMP, PTR)

This algorithm inserts TEMP as last node in the linked list. ITEM variable contains data of new node.

Step 1: Allocate memory for new node TEMP.

Step 2: [ Store the ITEM into INFO part of new node ]

TEMP →  INFO := ITEM

Step 3: [ Make the TEMP node points to NULL. ]

TEMP  →  LINK := NULL

Step 4: [Check whether list is empty or not. ]

If START = NULL then

START := TEMP

and Return.

[ End of If structure ]

Step 5: [ Initialize the PTR variable. ]

PTR := START

Step 6: [ Increment the PTR variable ]

Repeat while PTR  →  LINK ≠ NULL

PTR := PTR  →  LINK

[ End of Loop structure ]

Step 7: [ Insert the new node TEMP as last node. ]

PTR →  LINK := TEMP

Step 8: [ Exit ]

Return.

C.  Insertion of node after specified position

Algorithm: INSPOS (INFO, LINK, START, ITEM, TEMP, POS, C, PTR, PREV)

This algorithm inserts TEMP node after position POS in the linked list. ITEM variable contains data of new node.

Step 1: [Check whether list is empty or not. ]

If START = NULL then

Write (‘List is empty’)

and return.

[ End of If structure ]

Step 2: [ Initialize the PTR and C variable. ]

PTR := START

C := 0

Step 3: Repeat while PTR ≠ NULL and C ≠ POS

C := C+1

PREV := PTR

PTR := PTR  →  LINK

[ End of Loop structure ]

Step 4: If PTR = NULL and C ≠ POS then

Write (‘Position not found’)

and Return.

Step 5: Allocate memory for new node TEMP.

Step 6: [ Store the ITEM into INFO part of new node ]

TEMP →  INFO := ITEM

Step 7: [ Insert the new node TEMP. ]

TEMP  →  LINK := PTR

PREV  →  LINK := TEMP

Step 8: [ Exit ]

Return.

Searching of a Node in Linked List :

Algorithm: SEARCH (INFO, LINK, START, ITEM, POS, C, PTR)

This algorithm finds the position of a node containing the data ITEM and store it in variable POS.

Step 1: [Check whether list is empty or not. ]

If START = NULL then

Write (‘List is empty’)

and return.

[ End of If structure ]

Step 2: [ Initialize the PTR and C variable. ]

PTR := START

C := 0

Step 3: Repeat while PTR ≠ NULL

C := C+1

If PTR  INFO = ITEM then

POS = C and Return

[ End of If structure ]

PTR := PTR  →  LINK

[ End of Loop structure ]

Step 4: Write (‘ITEM not found’)

Step 5: [ Exit ]

Return.

Deletion of Node from Linked List :

A. Deletion of First Node

Algorithm: DELBEG (INFO, LINK, START, ITEM, TEMP)

This algorithm deletes the first node from the linked list and store it in TEMP. ITEM variable is used to store the data of deleted node.

Step 1: [Check whether list is empty or not. ]

If START = NULL then

Write (‘List is empty’)

and return.

[ End of If structure ]

Step 2: [ Store the data of first node into ITEM. ]

ITEM := START  →  INFO

Step 3: [ Remove the node ]

TEMP := START

START := START  →  LINK

Step 4: Free the TEMP node.

Step 5: [ Exit ]

Return.

B. Deletion of Last Node

Algorithm: DELLAST (INFO, LINK, START, ITEM, PTR, PREV)

This algorithm deletes the last node from the linked list. ITEM variable is used to store the data of deleted node.

Step 1: [Check whether list is empty or not. ]

If START = NULL then

Write (‘List is empty’)

and return.

[ End of If structure ]

Step 2: [ Initialize the PTR variable. ]

PTR := START

Step 3: Repeat while PTR  →  LINK ≠ NULL

PREV := PTR

PTR := PTR  →  LINK

[ End of Loop structure ]

Step 4: [ Store the data of last node into ITEM. ]

ITEM := PTR  →  INFO

Step 5: [ Deletes the node ]

PREV  →  LINK := NULL

Step 6: Free the PTR node.

Step 7: [ Exit ]

Return.

C. Deletion of Node Containing Particular Data

Algorithm: DELETE (INFO, LINK, START, ITEM, PTR, PREV)

This algorithm deletes the node containing the data ITEM from the linked list.

Step 1: [Check whether list is empty or not. ]

If START = NULL then

Write (‘List is empty’)

and return.

[ End of If structure ]

Step 2: [ Initialize the PTR variable. ]

PTR := START

Step 3: Repeat while PTR ≠ NULL

If PTR  →  INFO = ITEM, then

If PTR = START, then [ First node is to be deleted ]

START = START  →  LINK

Else:

PREV  LINK = PTR  →  LINK

[ End of If structure ]

Free the PTR node and Return.

Else:

PREV := PTR           [ Moving to next node. ]

PTR := PTR  LINK

[ End of If structure ]

Step 4: Write (‘ITEM not found’)

Step 5: [ Exit ]

Return.